Task-Space Control of a Medical Manipulator in Isaac Gym

Overview

This project studies classical control and task-space manipulation of a medical robotic arm using NVIDIA Isaac Gym, with the goal of understanding the strengths and limitations of analytical controllers before transitioning to learning-based frameworks such as Isaac Lab.

The emphasis is on simulation-first experimentation, focusing on control stability, task-space behavior, and GPU-accelerated physics rather than sim-to-real transfer.

Motivation

Recent advances in robotic manipulation increasingly rely on learning-based frameworks.
However, such approaches are best understood when grounded in classical control baselines.

This project aims to:

Establish a stable joint-space PD controller
Extend control to task-space (end-effector) objectives
Investigate Jacobian-based inverse kinematics
Expose controller limitations that motivate MPC and learning-based methods

Simulation Environment

Simulator: NVIDIA Isaac Gym (Preview 4)
Physics Engine: GPU PhysX
Platform: Ubuntu Linux with NVIDIA RTX GPU
Robot Model: Custom URDF-based medical manipulator
Control Loop: Fixed-step GPU simulation

The manipulator operates in a constrained workspace resembling medical tool navigation corridors.

Control Pipeline

Joint-Space PD Control

A classical proportional-derivative controller is applied at the joint level:

$\tau = K_p (q_{\text{des}} - q) + K_d (\dot{q}_{\text{des}} - \dot{q})$

This controller provides:

Stable simulation behavior
Correct DOF indexing
Proper torque application
Baseline dynamic consistency

Outcome:
Stable joint motion, but insufficient precision for constrained end-effector positioning.

Task-Space Control (End-Effector)

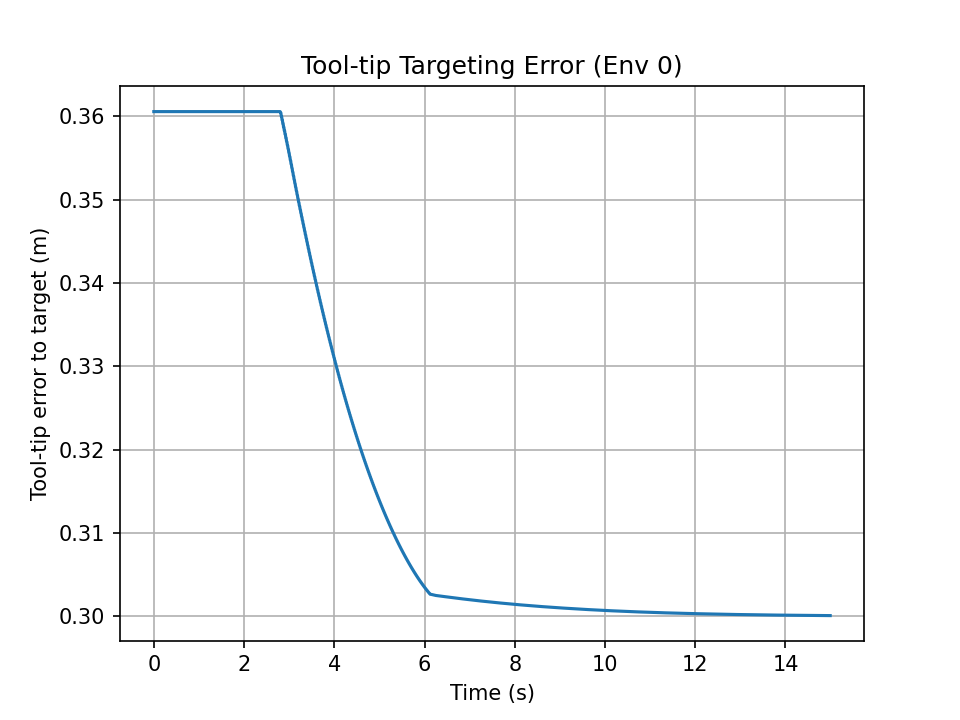
The task objective is defined in Cartesian space, focusing on the tool-tip position.

$ e = x_{\text{target}} - x_{\text{tip}} $

The controller attempts to reduce this error indirectly through joint torques.

Limitation:
Without explicit Jacobian reasoning, convergence is slow and constraint handling is weak.

Jacobian-Based Inverse Kinematics

A differential inverse kinematics controller is implemented using the manipulator Jacobian:

$ \dot{q} = J^\top \left( x_{\text{target}} - x_{\text{tip}} \right) $

This enables:

Explicit task-space reasoning
Directional joint updates
Improved alignment with end-effector goals

Observed Issues:

Sensitivity to Jacobian conditioning
Instability near singular configurations
No explicit handling of joint limits or obstacles

Results

The manipulator consistently moves toward the target, validating Jacobian-based control.
Precise convergence is not guaranteed in constrained environments.
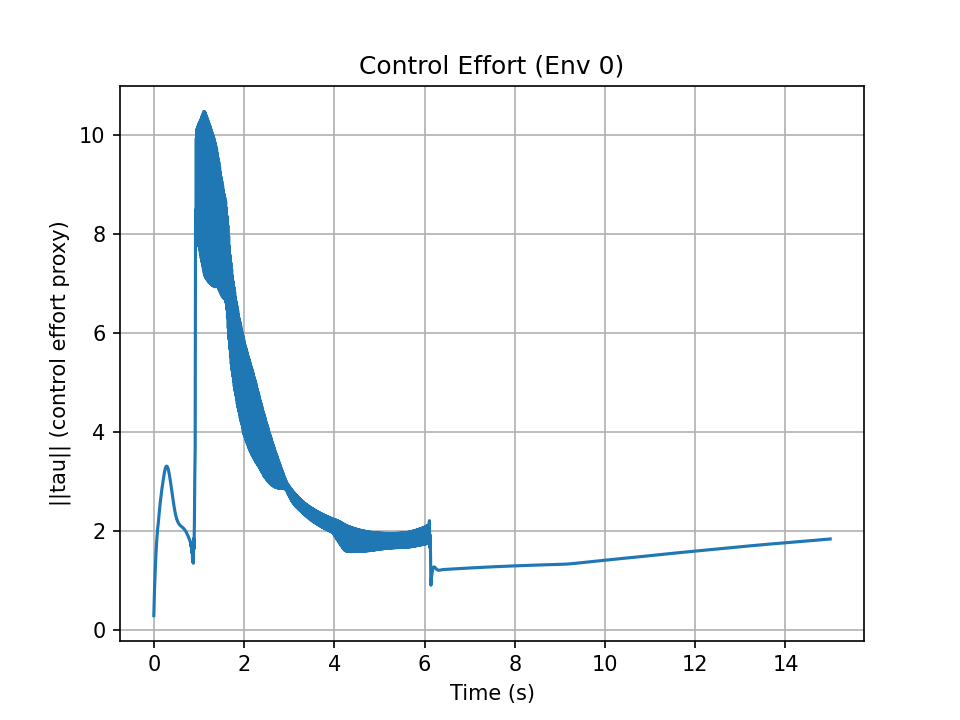
Oscillations and slow settling are observed under PD + IK control.

These behaviors highlight the fundamental limitations of purely analytical controllers in complex task spaces.

Key Insights

PD control ensures stability but not task completion
Task-space objectives require geometric reasoning
Jacobian-based IK improves directionality but lacks robustness
These limitations motivate:
- Model Predictive Control (MPC)
- Learning-based manipulation policies